C4

Optical and magnetic response of nanosystems using a semi-empirical many-body formalism

Antoine Honet¹, Luc Henrard¹, Vincent Meunier²

¹ University of Namur, Belgium
² Rensselaer Polytechnic Institute, Troy, NY, USA

In 1963, J. Hubbard introduced a model to describe electron correlations in solids. This model is an extension of the tight-binding (or Hückel) model, where we introduce an interaction term between electron of opposite spins located on the same site.

In his original paper, Hubbard used an Hartree-Fock, or mean-field (MF) approximation. The drawback of this approach is that it treats electrons as independent, neglecting all electronic correlations introduced by the model. The MF approximation is widely used to describe electronic and magnetic properties of solids.  However, correlations are of prime importance in electronic systems since they impact properties such as entanglement or plasmons (collective phenomena) but also the optical and magnetic properties of materials and in particular for the description of spintronic. For very small systems, it is possible to deal with the exact Hubbard Hamiltonian, by performing a so-called exact diagonalization (ED). However, this ED technique is computationally demanding since it has to be implemented in the many-body basis (instead of single-body basis) and its size grows exponentially with the number of electrons. There is thus a need for an approach that considers the correlations at a lower computational cost than ED. In this scope, Green’s function-based methods of many-body approximation (GFMBA) are of interest and consist of perturbation of non-interacting states in terms of Feynman diagrams. In particular, the GW approximation is a well-known approximation in the field of chemistry and ab initio computations.

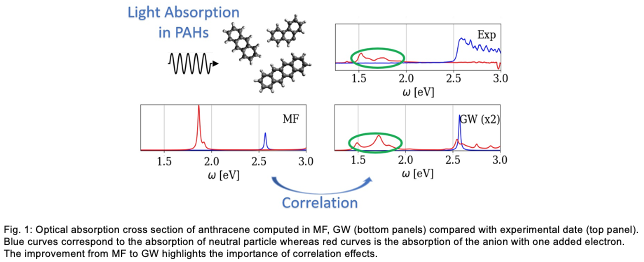
In our work, we implemented an algorithm to compute Green’s functions and GW approximation on top of a MF approximation, expressed in a tight-binding formulation [1]. This implementation allows to compute optical absorption cross-section of the considered material within MF approximation in a much faster way than the usually implementation. Then, it allows to compute optical absorption cross section from GW approximation Green’s functions. For small polycyclic aromatic hydrocarbon molecules, we showed that this absorption cross section, including correlation effects, are in much better agreement with experiment than the one obtained from MF approximation, in particular for the charged (open-shell) systems (see fig. 1).

 We also focus on very small systems that are accessible to the ED technique, such as linear chains. The goal is to compare the results of MF, GW and ED. We show that GW approximation leads to a better agreement with the exact result (ED) and we investigate some remaining shortcomings of GW approximation.

[1]        A. Honet, L. Henrard, and V. Meunier, “Semi-empirical many-body formalism of optical absorption in nanosystems and molecules,” Carbon Trends, vol. 4, p. 100073, Jul. 2021, doi: 10.1016/j.cartre.2021.100073.